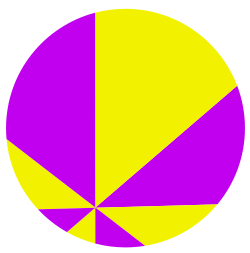
Теорема о дележе пиццы утверждает равенство площадей двух областей, получающихся при разрезании диска определённым образом.
Название теоремы отражает традиционную технику разрезания пиццы. Теорема показывает, что если два человека разрезают пиццу таким способом и по очереди берут куски, то каждый получит равное количество пиццы.
Утверждение теоремы
Пусть p будет внутренней точкой диска и пусть n будет кратно 4 и не меньше 8. Разрежем диск на n секторов с равными углами (равными 2 π n {displaystyle { frac {2pi }{n}}} радиан) по n 2 {displaystyle { frac {n}{2}}} прямым, проходящим через точку p. Пронумеруем сектора последовательно по часовой или против часовой стрелки. Тогда теорема о пицце утверждает, что:
Сумма площадей нечётных секторов равна сумме площадей чётных секторов .История
Теорема о дележе пиццы была первоначально предложена как задача-вызов Лесли Аптоном. Опубликованное решение этой задачи Майклом Голдбергом использовало прямое применение алгебраических выражений для площадей секторов. Картер и Вагон дали альтернативное доказательство путём разрезания. Они показали как нужно разрезать сектора на более мелкие кусочки, чтобы каждый кусочек в нечётном секторе имел конгруэнтный кусочек в чётном секторе и наоборот. Фредериксон привёл семейство доказательств рассечения для всех случаев (в которых число секторов равно 8, 12, 16, ...).
Обобщения
Требование, чтобы число секторов было кратно четырём существенно — как показал Дон Копперсмит, деление диска на четыре сектора или на число секторов, не делящееся на четыре, как правило, не даёт одинаковых площадей. Марби и Дайерман ответили на решение Картера и Вагона, дав более точную версию теоремы, в которой определяется, какой из наборов секторов будет иметь большую площадь, если площади не равны. В частности, если число секторов сравнимо с 2 (mod 8) и никакой из разрезов не проходит через центр диска, то подмножество кусков, содержащих центр имеет меньшую площадь, в то время как в случае, когда число секторов сравнимо с 6 (mod 8) и никакой из разрезов не проходит через центр, набор кусков, содержащих центр, имеет большую площадь. Нечётное число секторов невозможно при прямолинейных разрезах, а разрез через центр делает оба набора секторов равными по площади вне зависимости от числа секторов.
Марби и Дайерман заметили также, что в случае, когда пицца разделена поровну, то делится поровну и кромка (кромкой можно считать либо периметр диска, или площадь между границей диска и меньшим диском с тем же центром, при условии, что точка деления лежит в этом меньшем диске), поскольку диски, ограниченные обеими окружностями делятся поровну, то тоже будет и с их разностью. Однако, когда пицца разделена не поровну, едок, который получает большую часть площади пиццы, получает меньший кусок кромки.
Как заметили Хишхорны, равное деление пиццы приводит также к равному делению её начинки, если начинка распределена также в виде диска (не обязательно концентричного всему диску пиццы), содержащего центральную точку p деления на сектора.
Связанные результаты
Хиршхорны показали, что пицца, разрезанная как в теореме о пицце на n секторов с равными углами, где n делится на четыре, может быть разделены поровну среди n/4 людей. Например, пицца, разделённая на 12 секторов, может быть поровну разделена среди трёх человек. Однако, чтобы распределить пиццу на пять членов семейства Хиршхорнов, требуется разбить пиццу на 20 секторов.
Цибулька, Кинчл и др. и Кнауэр, Мичек, Ёкордт изучали игру выбора свободных кусочков пиццы в порядке, гарантирующем получение большей части, задачу, предложенную Даном Брауном и Питером Винклером. В версии задачи, которую они изучали, пицца делится радиально (без гарантии равенства углов секторов) и два обедающих поочерёдно выбирают кусочки пиццы, которые смежны уже съеденным секторам. Если два обедающих пытаются максимизировать количество съеденной пиццы, обедающий, берущий первый кусок, может гарантировать себе 4/9 всей пиццы и существуют разрезания пиццы, при которых он не может получить больше. Справедливый делёж или задача деления пирога рассматривает похожие игры, в которых различные игроки имеют различные критерии для измерения размера их доли. Например, один из едоков может предпочитать побольше пеперони, в то время как другой может предпочитать побольше сыра.

 Главная
Главная